• Triadic closure A-B，A-C 認識，則過一段時間後，B-C 很有可能也會互相認識
  
  也有可能跨多點連結，如 D-G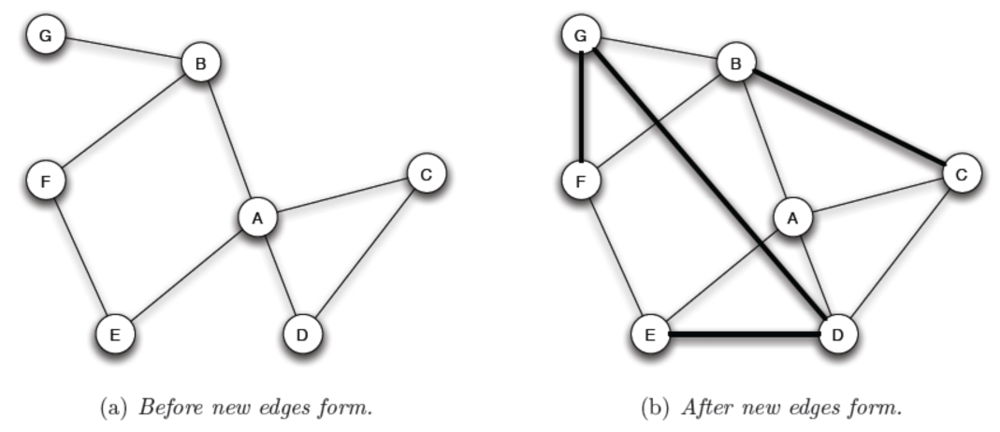
  
  • Clustering coefficient
    • $三角形/只有兩個邊的三角形$
    • 

Bridges - 連結兩個 component 的邊

Bridge

A-B 中間的即是 bridge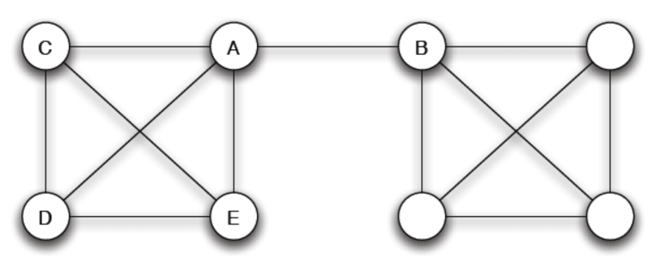

local bridge

但是 bridge 在社群網路上非常稀少，因此放鬆定義
兩個連線端點上無其他共同的點時，該連線即可稱為 local bridge
A-B 即是 local bridge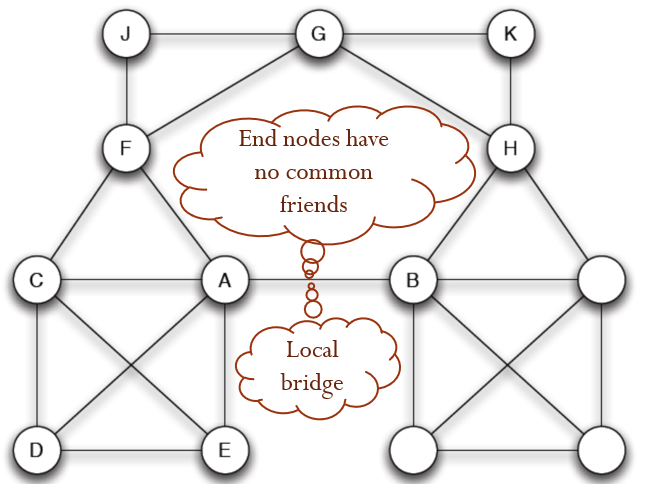

Span

當把 local bridge 刪除後 兩點的距離
span 一定 >= 3 (因為 local bridge 沒有共同點)

Bridge 類似於 Local bridge + 超大 span

Strong ties and weak ties

• Strong ties => 朋友
• Weak ties => 認識的人

Strong triadic closure property

如果 A-B，A-C 都是 strong ties，則 B-C 一定有 ties(strong or weak)
左邊滿足 Strong triadic closure property，右邊不滿足 Strong triadic closure property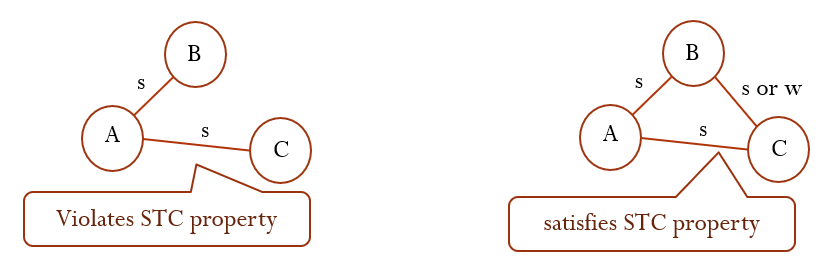

Local bridges and weak ties

如一個 點 A 所在的 graph 滿足 Strong Triadic Closure，有兩個以上的 strong tie，如果有 local bridge 則 local bridge 一定是 weak ties
用反證法來證明　　
假設 A-B 是 local bridge，根據 Strong triadic closure property，B-C 一定有邊，但這違反了 local bridge 的定義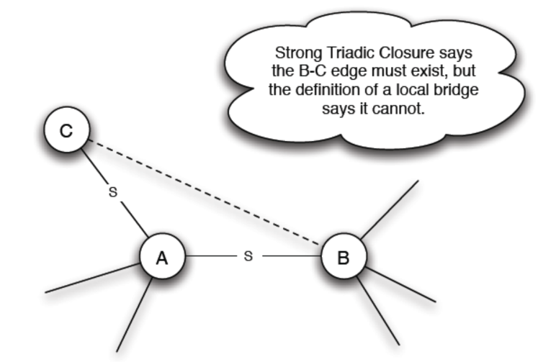

clusters

大網路內的 clusters 其內部大多是 strong，並透過 weak ties 跟其他 cluster 連接 下面章節會證明

Tie strength and network structure in large-scale data

因為 local bridge 實在太少，又放寬定義 定義 nearborhood overlap
$\dfrac{A \cap B}{A \cup B}$ !!注意 $A \ cup B$ 不包含 A B 本身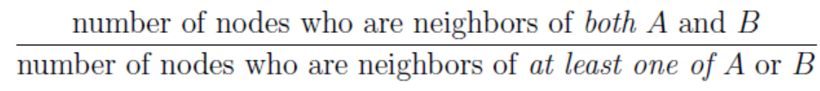

這樣還有個好處就是可以數值化ties 的強弱
Example A-F 的 overlap 只有 1/6 (C / B, C, D, E, G, J)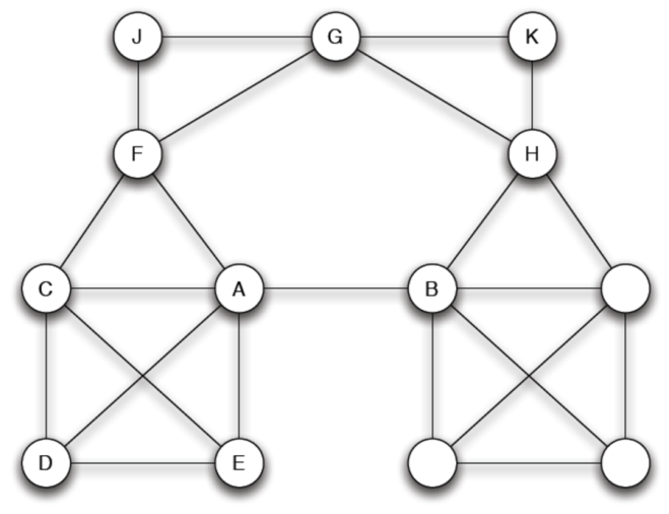

真實情況，確實 ties 強度(下方)跟 overlap(左邊) 是呈正比的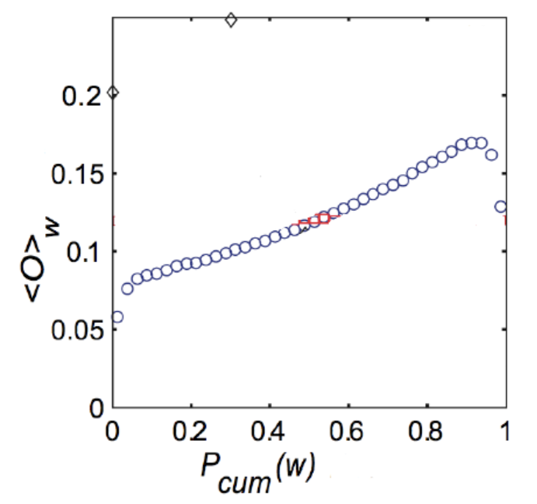

當把 weak ties 移除時， giant component 會縮小得很快

FB 上的探討

左上是所有朋友
右上是比較熟的人
左下是事件
右下是親密夥伴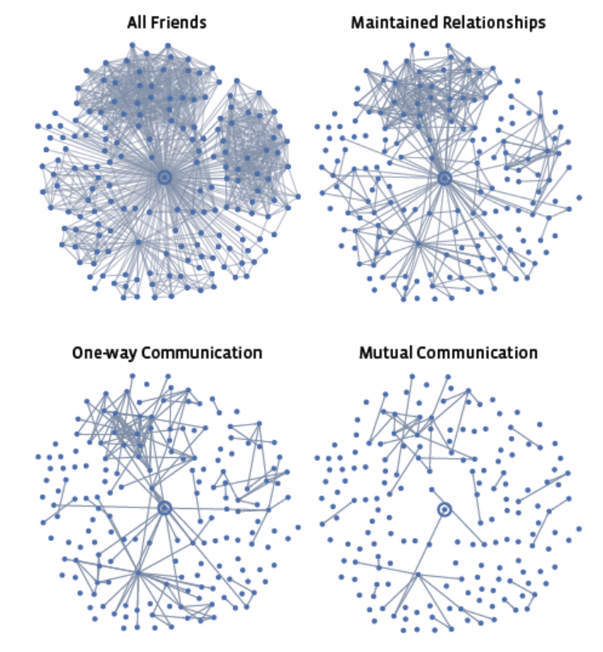

passive engagement - 介於 strong 跟 weak 中間的人

closure & structural holes & social capital

討論在社群網路中的位置提供的優勢

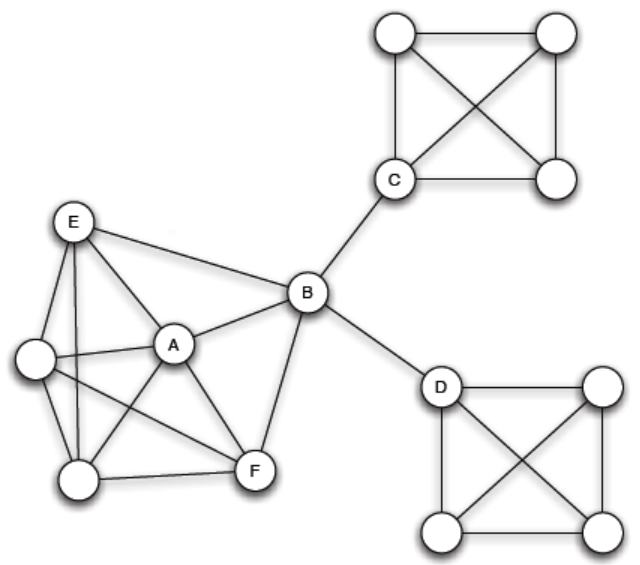
A 的 cluster coefficient 很高

Embeddedness

用處跟 cluster coefficient 類似 edge 兩端的 node 的共同朋友 A-B 的 Embeddedness 是 2

Tightly-knit groups

共同朋友越多 -> 互信程度越高

zero embeddedness

B-C 的 embeddedness 是 0

Structural holes

B 的位置稱為 Structural holes，像是E-B-C C-B-D 的空洞

B 的優勢

B 有機會拿到 early access - 拿到最新的外部訊息
B 有更好的 Creativity (因能獲得新想法)
B 也有機會過濾訊息 - social “gatekeeping”

social capital

• physical capital - 技術優勢
• human - 天賦
• ecoomic - $$
• cultural - 文化