Matching Markets - 市場交易

• 多人拍賣
• 人對不同貨品有不同程度的偏好
• 價格也是有偏好的
• allocation 可以是最佳的

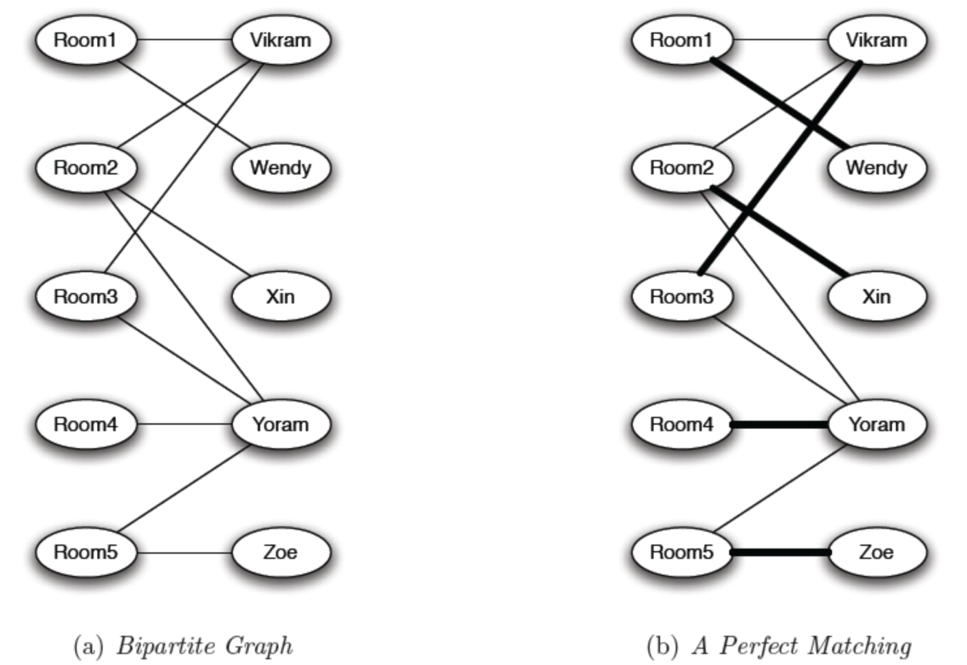
圖例

• 左邊是 賣家
• 右邊是 買家
• 實體線代表 賣家跟買家 之間有沒有可能有交易
• 粗線 代表達成交易
  

Perfect matching

要完成以下兩個條件

1. 每個 node 都要用粗線連線到對面
2. 一個 node 只能有一條粗線(即不能多點對一點)

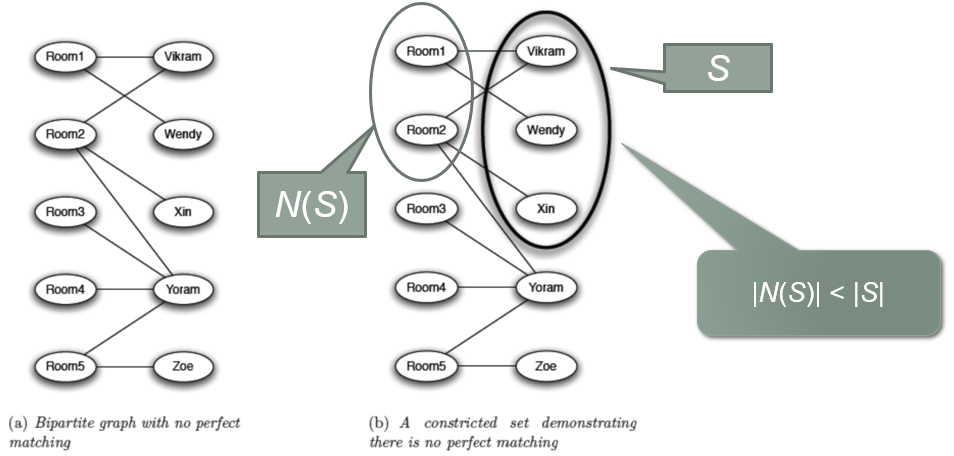
Constricted sets

1. 找出 seller set - $S$
2. 找出跟 $S$ 相連(near)的 node - $N(S)$
3. 如果 $|N(S)|$ 比 $|S|$ 小，則代表是 Constricted sets，即 $|N(S)|< |S|$
   

• 如果 $|N(S)|$ 比 $|S|$ 小，則不能能形成 perfect match，因為不可能將所有點連起來
• Matching Theorem - 如果 graph 中存在 Constricted sets，則代表這個 graph 沒有 perfect match

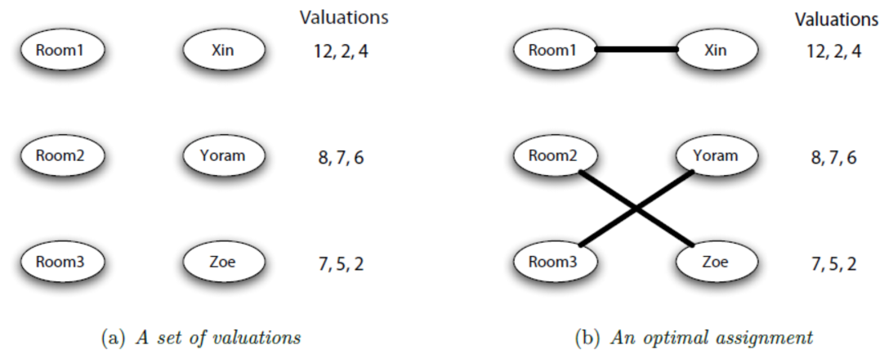
Valueation & optimal assignments - 加上偏好程度

• 右邊數字分別代表買家對 seller 1 2 3 的偏好(value)
• Quality - 所有買家的偏好相加
• optimal assignment - 買家偏好要最高
  

如果是 binary 的話，就只是 value 變成 0 跟 1 而已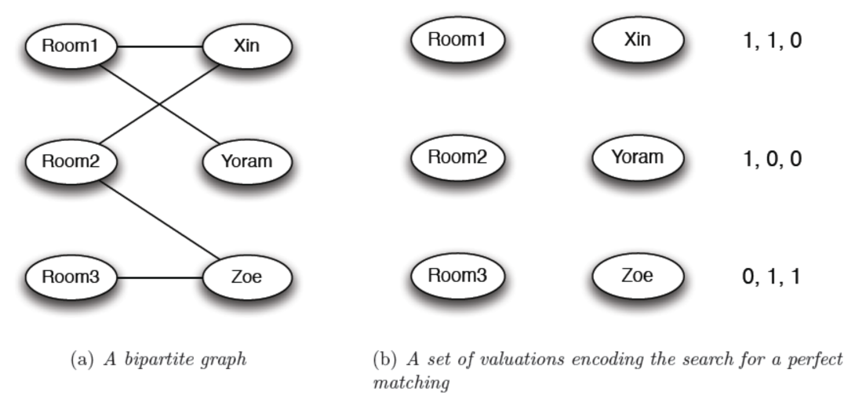

Price - 加上售價

• 如果左邊出價格 p ，如果 value - price < 0，那 payoff 就是 0 (因為可以不買)
• 買家想要最大化他的 payoff，即 value - price

preferred seller - 這個 buyer 偏好的 seller

即使買家 payoff 最大化的賣家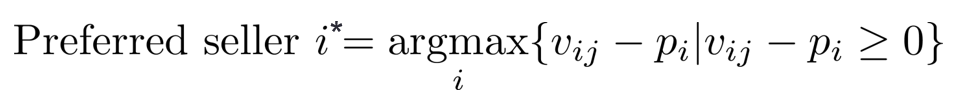

preferred-seller graph & market clearing

所有 buyer 跟其 preferred-seller 都連起來的 graph
當 preferred-seller graph 能夠形成 perfect graph 就稱為 market clearing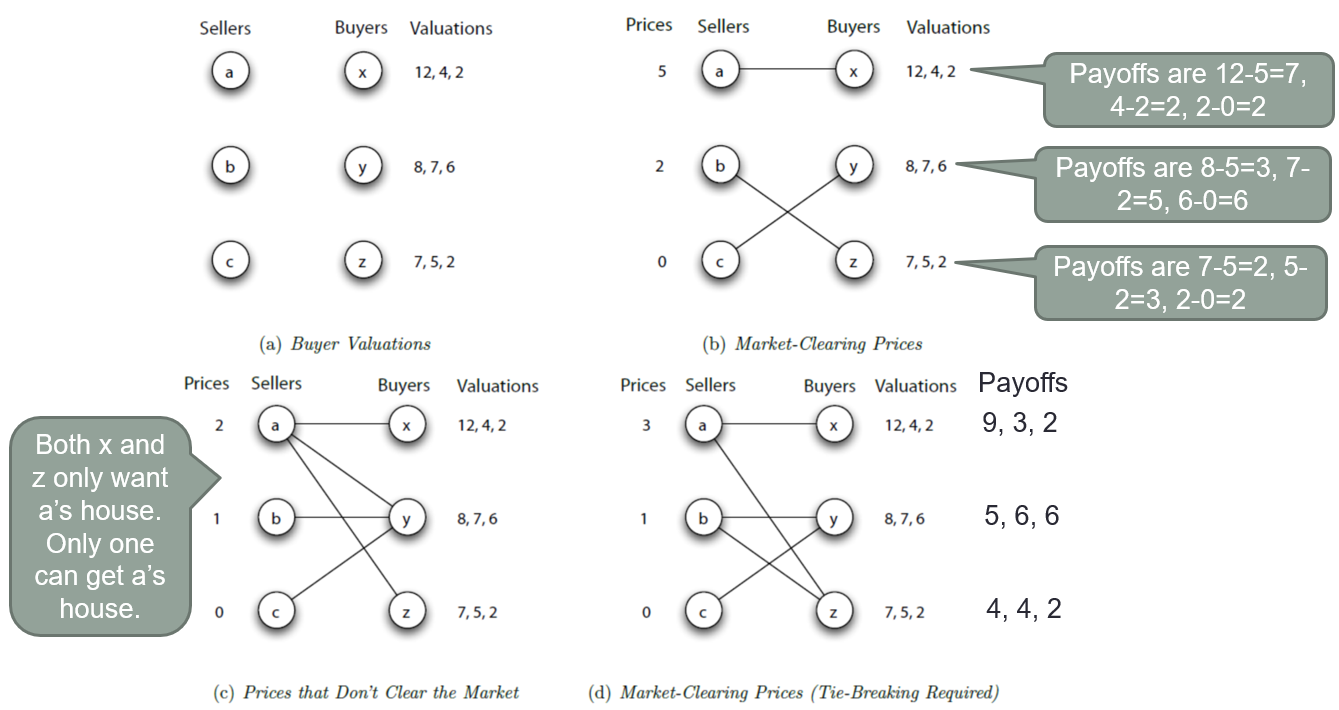

兩個問題

1. clear market 時， quality 好不好
2. 給定任意的買方偏好價格，是否一定存在 prefect matching (buyer 跟 seller 數量要相同)

1 clear market 時， quality 好不好

定義 total payoff M 是下面這樣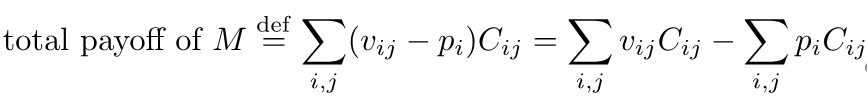

$\sum_{i,j}v_{ij}C_{ij}$ - M 的 total value
$\sum_{i,j}p_{i}C_{ij}$ - 所有價格相加 (因為價格不會因為不同連線方式改變，所以是個常數)

當 clear market 時，每個 buyer 都一定是連到 perfect-seller (因 preferred-seller graph 是成立 market clear 的先決條件)，因此 M 的 total value 一定是最大值，而 payoff 相加是個常數，因此會是最大值

2 作者稱之為 bipartitle graph auction model

演算法

1. 每個 seller 初始價格為 0
2. 建立 perferred-seller graph
3. 如果已經 market clear 了，那就做完了
4. 不然就找一個 seller set S 的 constricted set
5. 把 N(S) 的 buyer 的售價全部 + 1
6. 將所有 seller 的售價減去所有 seller 售價的最小值， $p_i - min(p_1, p_2 …, p_n)$
7. 重複做上述步驟，直到找到 perfect matching

如下圖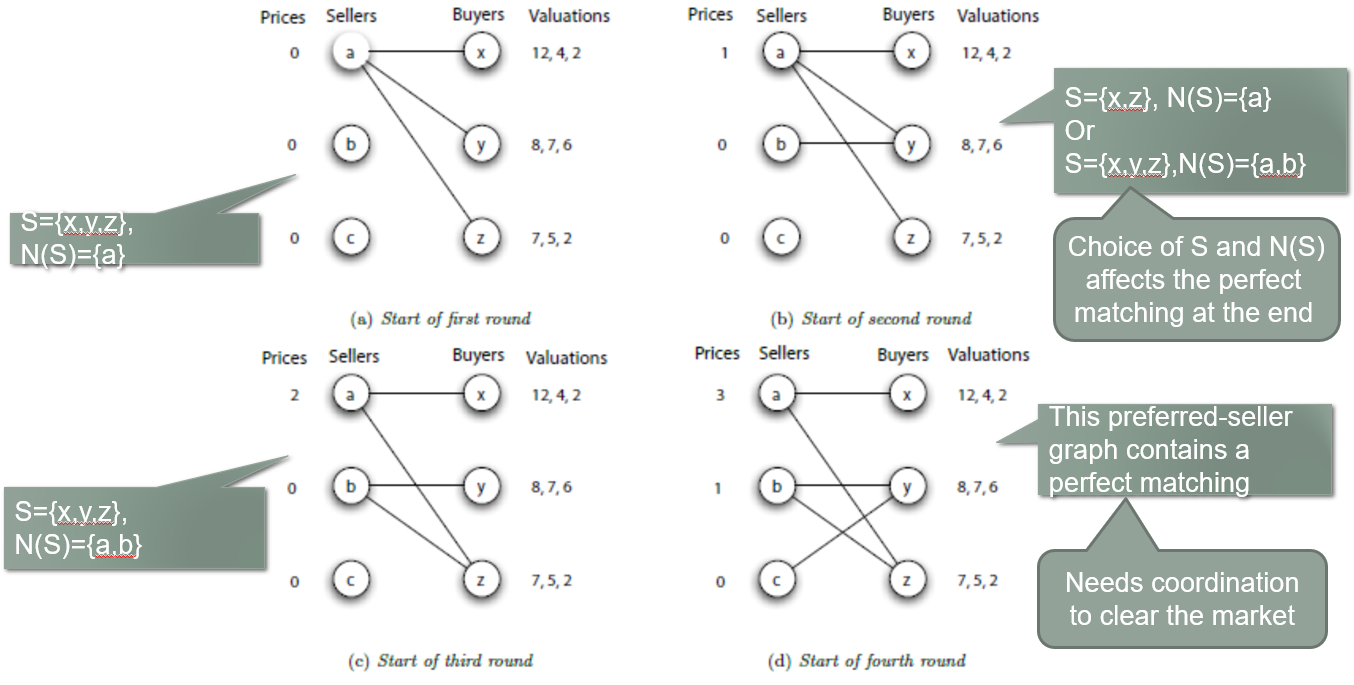

那這會停止嗎? 會，因為這如同位能一樣，只會遞減，不會增加。 且最小值又是 0 ，因此迭代次數夠多的話就一定會停 (因為只會遞減)

定義位能 (potential)

• 買家位能 = 買家的 payoff
• 賣家位能 = 賣家的出價
• 交易位能 = 買家 + 賣家的位能

證明

1. 初始位能都 >= 0
   1. 因為初始所有 seller 初始 potential 都是 0
   2. 所有 buyer 的 payoff 都是正的 (因 seller 售價都是 0)
2. 會影響 potential 只有 step 5 跟 step 6
   1. step 6 - 因為 buyer 跟 seller 的 potential 會抵消，因此不影響 potential
   2. 因為 $|S| > |N(S)|$，故 整體 potential 會下降

將 single-item auction 轉匯成 multi-item auction

建立很多 fake additional seller，其他買家對 fake seller 的 value 都是 0
如下圖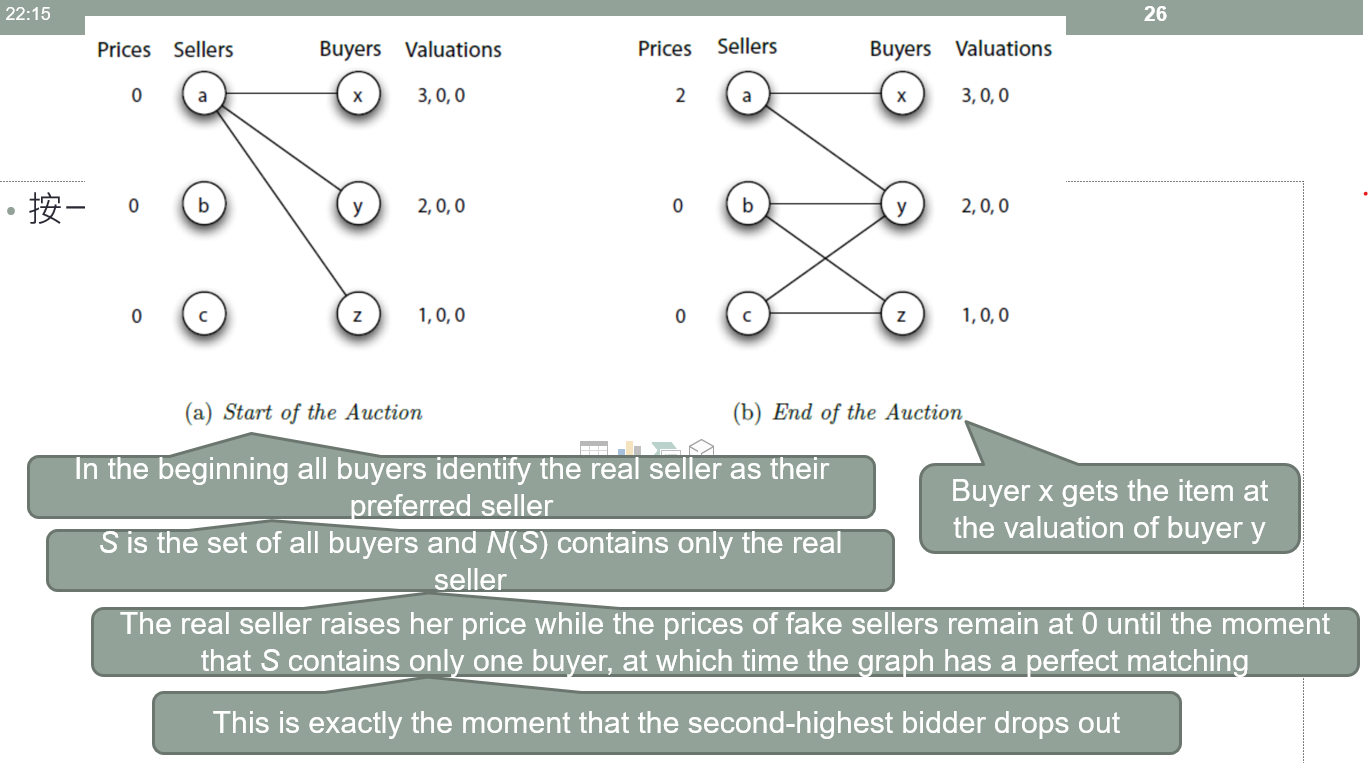

當 market clear　時，很像是 auction 的 Sealed-bid Second-price price