May 31, 2020

社群網路筆記 CASCADING BEHAVIOR IN NETWORKS

網路中的擴散 Diffusion in networks

  1. 跟考慮整個人群比起來，考慮細粒度的傳播，就是跟考慮整體決定比起來，通常會比較關注身旁的人的所下的決定
  2. 考慮在 graph 中的擴散
  3. 也稱為 diffusion of innovations

人們模仿鄰居的原因有兩個

  1. Informational effects - 發現鄰居做了 A 行為後得到好處，每個人的收益都不受他人影響，目前研究結論有
    1. 創新，缺乏了解，使採用它具有風險
    2. 能獲得很高的利益，所以人們才採用
    3. 越早採用的人，社經地位通常越高，交友程度通常越多
    4. 是否採納通常藉由觀察鄰居決定
    5. 無 direct benefit effect
  2. Direct-benefit effects - 發現鄰居做了 A 行為後得到好處，且越多人做收益越大，具有以下特性
    1. 吸引人的兩大原因
      1. 專家採用
      2. 大多數人採用
    2. 可以傳播開的原因
      1. Complexity - 不太複雜
      2. Observability - 很容易觀察到好處
      3. Trialability - 試用風險小
      4. 符合社會的習慣

diffusion through a network 的模型

  1. 用傳染病模型模擬
  2. 用 direct benefit effect 模型模擬，這裡使用這個模型，特色有
    1. 越多人採用，收益越高
    2. 出於自身利益，當足夠多鄰居採用時才應該採用

direct benefit effect

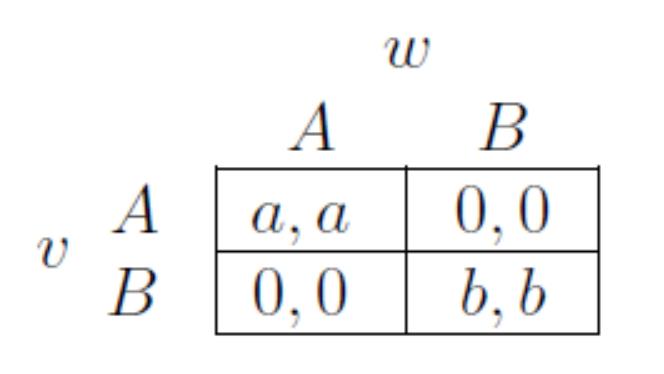
  1. 跟所有鄰居玩 coordination game coordination
  2. 點 v 的 payoff 是跟所有鄰居玩 coordination game 的和，v 也是基於和來做決策
  3. p 是 v 的鄰居中採用 A 的比例， d 是鄰居數量， a b 則是不同 coordination game 選擇的 payoff 當 node v 採用 A 時 $pda\geq(1-p)db$，否則採用 B 就是 $pda\leq(1-p)db$ 可變成 $p\geq\frac{b}{a+b}$，定義 $q=\frac{b}{a+b}$

實驗

  1. 假設 B 是舊的策略，A是新東西
  2. 一開始有些人會開始採用 A
  3. 其他人會開始慢慢轉變成 A

TODO proof 過程中 只會從 B 變成 A，A不會變回 B

問題

  1. 所有人都會變成 A (complete cascade)
  2. 如果不是，那不變成 A 的原因是什麼

新思想很難傳播進 tightly-knit 的社群 (內部連接緊密，外部連接稀疏)

  • 現實中像是以下原因都會造成 tightly-knit 的社群
    • 不同年齡層
    • 不同生活習慣

繼續傳播的策略

  1. 提高 A 的質量， 讓 q 門檻下降，像是 a 從 3->4，q就會從 2/5 -> 1/3
  2. 讓 tightly-knit 的社群 內部有些節點開始轉換
    1. 衍伸出新問題，要怎麼選那些點轉換

把 tightly-knit 用數學定義表示

cascade 可以傳播多遠，取決於

  1. 新技術的優點
  2. 社群連接的緊密程度

定義 cluster

  • a cluster of density p ， 就是一組(set) node，每個 node 至少有 p 比例的鄰居在這個 set 當中
  • 網路中可同時存在多個規模的 Clusters
  • 缺點是
    1. p =1 的定義不好，因為所有點都在內的話也滿足 p =1 的定義
    2. 即便兩個 p cluster 沒有連接，但兩個在一起也滿足定義

宣稱

  1. remaining network 就是不包含初始點的點的集和
  2. 若初始點採用 A，且轉換門檻為 threshold q，則
    1. 如 remaining network 包含 1-q 的 cluster，就不會是 complete cascade
    2. 如果不會是 complete cascade，則remaining network 一定有包含 1-q 的 cluster
    3. 1-q <=> complete cascade

證明

如 remaining network 包含 1-q 的 cluster，就不會是 complete cascade

proof 1-q 的 cluster 是 complete cascade 的阻礙 反證法 假設有個大於 1-q 的 cluster 有個 node v 在其中，且是第一個變成 A 的 node 因 v 在 大於1-q cluster　中，所以外面最多也就 小於 q 比例的 node，因此最多也就 小於 q 比例的 node 採用 A，因此 v 不可能轉變成 A

如果不會是 complete cascade，則remaining network 一定有包含 1-q 的 cluster

proof 1-q 的 cluster 是 complete cascade 的唯一阻礙 假設 S 是最後依然不轉變的 cluster 要證明 沒有轉換的 S 的 density 比 1-q 大

假設 w 在 S 中，不會轉變，因為她的鄰居最多也就 小於 q 會採用 A 而 w 有 1-比例的鄰居採用 B，且都在 S 中 因此，就定義而言， S 就是有 1-q density 的 cluster

實驗結論

從接收到消息跟實際採用會需要一段時間
門檻低的消息容易傳送， weak ties 也比較容易傳播門檻低的消息

每個 node 都有自己的 a b

跟之前類似，不過要分開考慮
blocking cluster ，就是跟之前的 1-q density 類似，只是條件是每個在裡面的 node v 的 $1-q_v$ 比例的鄰居也在 blocking cluster 內

comments powered by Disqus