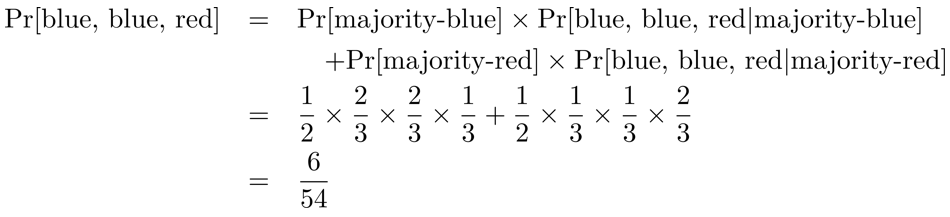Information Cascades

簡介

當自身有資訊，且也獲得別人跟你說的資訊時，是要依照自己的資訊做決定還是跟別人一起做

• herding 、 information cascade、social contagion - 不依照自己獲得的資訊做決策，而是跟別人一起做
  • 不是單純模仿(imitating)
  • 也不是盲從(not mindless)
  • 也不是因為社交壓力(social pressure)
  • 而是經過計算後的決定 !!
  • 人越多，越容易傳播
• Information effects - 別人只影響你下決策而已，不影響下完決策後能獲得的利益
• Direct benefit effects - 別人除了影響你下決策之外，更會影響下完決策後能獲得的利益
  • 例如電話普及之前，越多人使用，你就能跟越多人聯絡，因此越多人用，電話給你的利益越大

實驗

實驗環境

• 實驗前告訴每個人，箱子裡的球是 兩藍色一紅色 或 兩紅色一藍色 的機率各半
• 每個人輪流上台抽球，並告訴大家他覺得箱子裡的球是哪種顏色比較多
• 每個人都只能看到他自己抽的球

推論

1. 第 1 號人，抽到啥顏色就猜主要是啥顏色，例如抽到藍色就猜藍色
2. 第 2 號人，
   1. 如抽到跟 1 號相同，就猜跟 1 號相同的顏色
   2. 如果不同，就猜自己抽到的顏色
3. 第 3 號人，
   1. 如果前兩者一致，說明箱子裡那個顏色的機率比較大，無論自己抽到啥顏色，都會猜跟前兩者一樣的顏色 - information cascade
   2. 如前二不一致，猜自己看到的顏色
4. 第 4 號人，
   1. 他知道第 3 號有可能受到 information cascade，因此只有前兩號資訊是真的，所以 4 的決策資訊跟 3 相同
5. 4 之後都跟 3 一樣

結論

• information cascade 容易形成 - 只要前兩個顏色相同，後面就會全部都猜一樣的顏色。全錯機率有 1/9
• cascade 也是脆弱的，如果中間有兩個人亮出抽到的不一樣顏色球給所有人看，那 cascade 就會被打破，因為有用資訊就變成 兩藍兩紅
• 但是如果是 direct benefit effect 的 cascade 就很難打破了

數學表示

主要是條件機率
$P[主要藍色|抽到甚麼顏色]$ 的機率 大於 1/2 時，就應該猜藍色$

第一人

$P[主要藍色|抽到藍色] = \frac{P[主要藍色]P[抽到藍色|主要藍色時]}{P[抽到藍色]} = \frac{\frac{1}{2}\frac{2}{3}}{\frac{1}{2}}=\frac{2}{3}$

其餘類似

第三人

$P[主要藍色|抽到藍色 藍色 紅色] = \frac{P[主要藍色]*P[抽到藍色 藍色 紅色|主要藍色時]}{P[抽到藍色 藍色 紅色]} = \frac{ \frac{1}{2} * ( \frac{2}{3}^2 * \frac{1}{3} ) }{\frac{6}{54}}=\frac{2}{3}$