定義

• True Value - 每個 bidder(買家) 都有自己的估價，買家不會買超過自己估價的東西

四種拍賣方式

1. Ascending-bid auction - 買家喊價，越出價越高，最高價者得標
2. Descending-bid auction - 賣家喊價，價格越喊越低，直到有人接受
3. First-price sealed-bid auctions - 同時出價，價格最高者得標，並付出喊價的價格
4. Second-price sealed-bid auctions - 同時出價，價格最高者得標，並付出喊價次高者喊的價格

拍賣適合的時機

!! 買賣雙方都不知道真實的價格 !!

如果買方知道賣方的估價，就直接用賣方估價買就好了
如果賣方知道買方的估價，就直接用買方估價賣就好了

拍賣方式的關係

Descending-bid auction 跟 First-price sealed-bid auctions 在數學上是一樣的
因為假設 bidder 估價為 b，當賣方逐步降價時，如果降到有 bidder 能接受的價格 b 時，該 bidder 就會買下

Ascending-bid auction 跟 Second-price sealed-bid auctions 在數學上是一樣的 因為假設 bidder 估價為 b，當買方逐步出價時，估價最高的 bidder 將會贏的拍賣，且因為是逐步出價的，所以最高出價的買方只要贏過次高出價的買方就好了，不需要出到自己的估價，因此跟 Second-price sealed-bid auctions 相同，贏得拍賣，並付出次高買方喊的價格即可

!!! 改變規則會改變行為，因此 first-price 跟 second-prie 的收益會相等 !!!

數學符號

• bidder - 買家
• $b_i$ - 第 $i$ 個買家的出價
• $v_i$ - 第 $i$ 個買家的估價
• $b_i$ 的 payoff
  • 如果贏了，則是 $v_i - b_i$
  • 如果輸了，則是 $0$
• truthful bidding - 出的價格就是估價

Second-price auctions

!!! Sealed-bid Second-price price auction 中，每個 bidder 的 dominant strategy 就是出自己的估價

Tie breaking

如果前兩大的出價相等的話，要怎麼決定哪個能得標呢?

1. 用說好的順序決定輸贏
2. 假設同樣價差之間差距 $\varepsilon$，而 $\varepsilon\approx0$

證明 truthful bidding 在 second-price sealed-bid auctions 中視最好的策略

觀察

1. 要證明 $b_i=v_i$ 時，沒有其他 $b_i’$ 能夠比 $b_i$ 還要好
2. $b_i$ 有兩種方式可以做偏移，上升或下降
3. $b_i$ 只影響輸贏，不影響 payoff

分段證明

第一章圖是教科書的證明，第二張圖是我自己的想法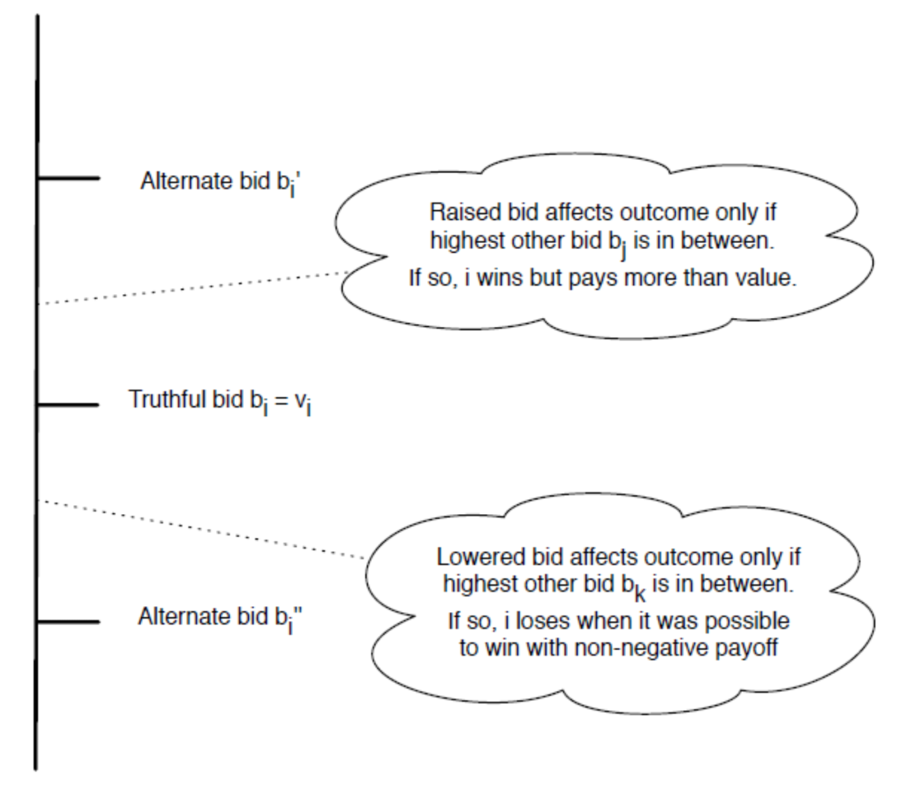

First-price auctions

• 如沒有贏， payoff 就是 0
• 如果贏了， payoff 就是 $v_i-b_i$

因為 payoff 會隨 $b_i$(出價) 改變，因此 truthfulness 就不再是 dominant strategy
也因此我們要把 bid 壓越地越好，但是要盡可能的贏得拍賣

All-pay auction - 即使沒贏，也要付出代價

• 如出價 $b_i$ 沒有贏， payoff 是 $-b_i$
• 如出價 $b_i$ 贏了， payoff 就是 $v_i-b_i$

all pay auction 的 optimal bid 跟 first-price auction 類似

Common Values & winner’s curse

• Common Values - 物品有實際價值，但沒人知道實際價值是多少，像是油田等等
• winner’s curse - 如果買家的估價比實際價值高，那當買家實際開採或轉賣時，很可能賠錢，又因為是最高者得，所以買家高估實際價值的可能性比較高
• 也因此就算是 second-price auction，truthful bidding 也不會是 dominant strategy， 因為物品具有實際價值
• 因此 購買時要考慮 winner’s curse

模型

• $v_i$ - 估價
• $v$ - 實際價值，但沒人知道實際價值是多少
• $x_i$ - 誤差 $v_i = v + x_i$