May 7, 2020

社群網路筆記 power & bargaining

社群網路筆記 power & bargaining

Power - 影響力

個人屬性、在網路中的位置，等等都會造成影響力
有些研究者認為影響力是相對的，而不是絕對的

Network Exchange theory

Social exchange

edge 上的 value 怎麼分配給兩個 node
而此時 social exchange 的不平均程度則反映了 power 的相對程度

探討位置造成分配不均的問題就是 network exchange theory

造成分配不均的原因

如 B > A，則有可能是因為

  • Dependence - A 依賴 B
  • Exclusion - B 有能力排除 A
  • Satiation - A 要給 B 更多資源才能使 B 滿意
  • Betweenness - A 到其他點的最短路徑會包含 B(但是也有 Betweenness 越大， power 越小的反例)

one-exchange rule

同一個 Node 只能跟鄰近的 一點 來分 Value (跟 matching 有點像)
如 A-B 且 A-C，則 A 只能跟 B 或 C 分 Value

實驗的一些術語

  • High-information - 能看到所有人的交談結果
  • Low-information - 只能看到自己周圍的人的交談結果

實驗結果

  • Two node path
    • A-B
    • 50%-50%
  • Three node path
    • A-B-C
    • (1/6)-(5/6)-0 or 0-(5/6)-(1/6)
  • Four node path
    • A-B-C-D
    • B C 大約能站 7/12 ~ 2/3
  • Five node path
    • A-B-C-D-E
    • C 只比 A E 好一些
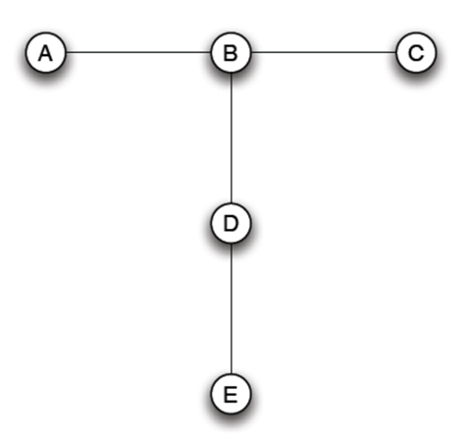
  • fig12-1
    • D 不會跟 B 連，D 跟 E 大概五五分
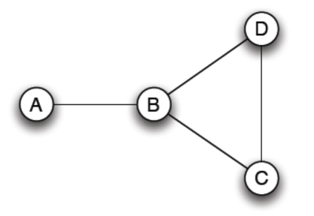
  • fig12-3
    • D C 五五分，B 比 4 node 的 B 稍大一點
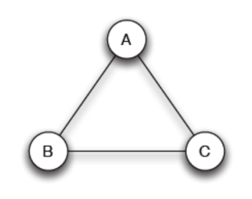
  • fig12-4
    • unstable network or unpredictable outcome
    • 永遠都不會停

跟 buyer-seller-network 做連結

把一條 path 轉成左右左右
但是限制很多

  1. node 要是偶數
  2. 不是任何結構都能轉成 bipartite，而且這只是數學表達方式相同而已

建立數學模型

Nash bargaining solution

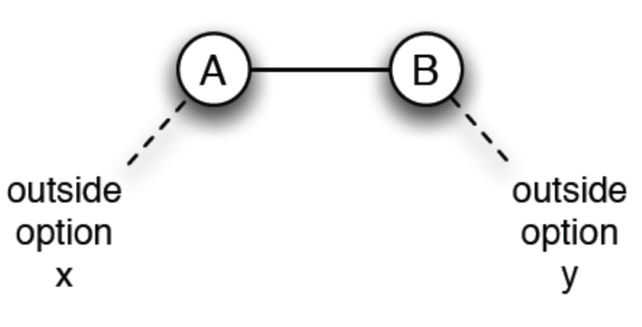
nash bargaining

如談判失敗，A 拿到 x，B 拿到 y
如 x+y > 1，因為拿到 outside value 會使 A B 拿到最大利益，則 A B 永遠不會考慮協商
所以如果能談派的話，surplus(剩餘價值 s) = 1-x-y >= 0
且談判技巧相當的話，A B 將會平分剩餘價值 s
因此 A 的 outcome 是 $A=x+s/2=(x+1-y)/2$
B 的 outcome 是 $B=y+s/2=(y+1-x)/2$

equi-dependent outcome - 互相依賴

如果 outside option 越大，則拿得越多

inflate - 虛張聲勢，使人高估 deflate - 使人低估

The ultimatum game - 最後通牒

A 提出分法，B只能選擇接受或拒絕，如果接受就成交，不接受就談判破裂，雙方都不會獲得任何東西

在完全理性的情況下，A 會提出 A 0.99，B 0.01 這樣的分法
但實際實驗，A通常只拿 1/2 ~ 2/3，因為要考慮情緒

outcome

outcome 包含兩件事情

  1. 哪兩個 node 分
  2. value 怎麼分

stable

stable 定義: 當沒有任何 node X 能提出 offer 使 x y 都獲得更好的 outcome
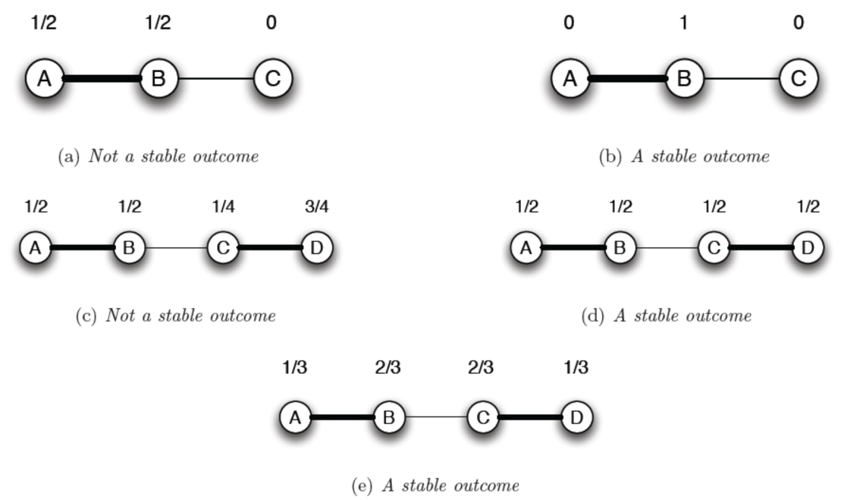
當滿足 stable 時，不在 match 中的 edge，其兩端的 node 的 outcome 相加要大於 1，如果小於 1 ，代表該還有多的 value 可以分給兩端的 node stable
擅長找到分配極端不均的情況
實際實驗中， 1/6 5/6 就算是極端不平均了

三角形網路不會有 stable outcome

缺點是 stable 網路有很多可能 例如四個點的，可以 (1/2)-(1/2) 或 (1/3)-(2/3) 分，但是均分那個比較不合理(因 B 是優勢位置，應該會拿到更多才對)

balanced outcome

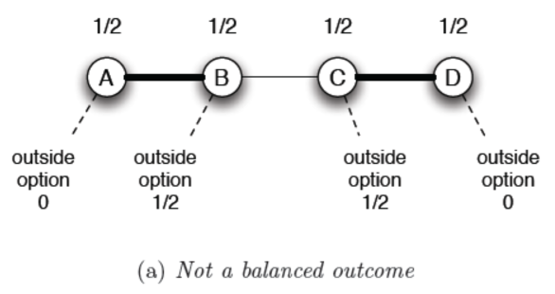
考慮 用 outside options 來擴充 nash bargaining solution，變成 balanced outcome B 的 outcome 是 1 - C 的 value = 1- 1/2 = 1/2 balanced

  • balanced 是 stable 的子集合，即是 balance 則一定是 stable
  • 如 B 同時跟 A B C D 連結，則 B 的 outside solution　是　max(1-C, 1-D, 1-E)

其他研究

  • stable 跟 blanace 可以用 cooperative game 表示
    • stable 可以用 core solution 表示
    • balance 可以用 kernel solution 表示
  • equiresistance - 其他可解釋 outcome 的理論

Dynamic Game 在特定情況下跟 bargaining solution 一致

  • finite-horizon problem - 時間有限，由後往前推論
  • infinite-horizon problem - 時間無限，由前往後推論

infinite-horizon

第一輪 A 出價，B決定要接收或拒絕
第二輪換 B 出價，A 決定接受或拒絕
為了避免無限進行，引入 breakdown probability p ，每輪結束後有 p 的機率會直接結束 game

  • 因為可以計算，所以通常第一輪 A 的提議就會被接受
  • 如果 p 很小，造成結束的原因是因為達成協議
  • 這裡只考慮一個 edge 兩個 node
  • 多個 node 還是研究的議題

分析 finite-horizon problem

只做兩輪的情況

Round 2(B 提 offer)

B 只要給 A x(A 的 outside value) 就好，因為 A 不接受，遊戲就直接結束，A 也只能拿到 x
因此 B 可以留下 1 - x

Round 1(A 提 offer)

A 計算 B 的期望值是 $z=py+(1-p)(1-x)$， $py$ 是第一輪就 breakdown 的狀況， (1-p)(1-x) 是沒有 breakdown 的情況
因此 A 只要給 B z 就好，A 留下 1-z， 1-z > x

B 的 payoff 是 $z=py+(1-p)(1-x)$，

  • 當 p 趨近 1，對 A 有利，
  • 當 p 趨近 0， A 拿走的量很接近 A 的 outside option
  • 當 p = 0.5 則 接近 Nash bargaining outcome

infinite-horizon problem

  • stationary strategies - 假設策略不隨時間改變
  • stationary strategies 達成的平衡稱為 stationary equilibria

A 提出 $(a_1,b_1)$，B 只會在 $b_1>=z_B 時接受$
B 提出 $(a_2,b_2)$，A 只會在 $a_2>=z_A 時接受$

by 之前 Round 1 的分析，且 $(1-z_A) = b_2$ ，可知 $b_1 = z_B = py+(1-p)(1-z_A) = py+(1-p)b_2$ 相對的
$a_2 = z_A = px+(1-p)(1-z_B) = py+(1-p)a_1$

因此可得 $a_1=\dfrac{(1-p)x+1-y}{2-p}$
$b_1=\dfrac{(1-p)y+1-x}{2-p}$
B gey payoff 是
$b_1=1-a_1=\dfrac{y+(1-p)(1-x)}{2-p}$

當 p 接近 1 時， $(a_1,b_1) \approx (1-y,y)$
當 p 接近 0 時，game 會持續很久， payoff 是 $(\dfrac{x+1-y}{2} ,\dfrac{y+1-x}{2} )$

comments powered by Disqus