Direct benefit effect OR Network effect

INformation Cascade 中影響人們決策的原因有兩個

1. Information effect - 只影響考慮過程，不影響行動後獲得的利益
2. Direct benefit effect 或是 Network effect - 除了影響考慮的過程，更影響行動後獲得的利益

• Network effect 是外部因素(externalities)，可以是正或者是負的
• Network effect 會影響別人的 welfare(payoff)，但不是直接影響(uncompensated)，而是間接影響
  • 直接影響就是你買東西別人不會給你錢
  • 間接影響就是越多人用這東西對你價值越高，例如社群網路
• 本章節的 welfare 是看使用者的數量

The economy without network effects

先討論不具有 network effect 的商品，再來討論具有 network effect 的商品

1. 假設這是個很大的市場，裡面有很多小的 consumer 跟 producter，每個對市場的影響都很小(價格不會波動)

2. 用 0~1 的實數代表無限多的 consumer(好處是能很方便回答 0~x 有 x 人)

3. 每個 consumer 只要一個商品

4. 每個 consumer 都有其 Intrinsic interest(偏好)

   1. Reservation price - 量化的 intrinsic interest
   2. consumer 的 Reservation price 由高到低排下來，及 consumer 0 的 reservation price 是最高的
   3. 用 function r 代表 reservation，r(0) 代表 consumer 0 的 reservation price
      1. 由 4-2 可知 r(0) > r(0.1) > r(0.5) > r(1)
      2. r 是嚴格遞減，即沒有一樣的 reservation price
      3. r 稱為 inverse demand function
      4. r 的反函數 $r^{-1}$ 稱為 demand function
      5. 

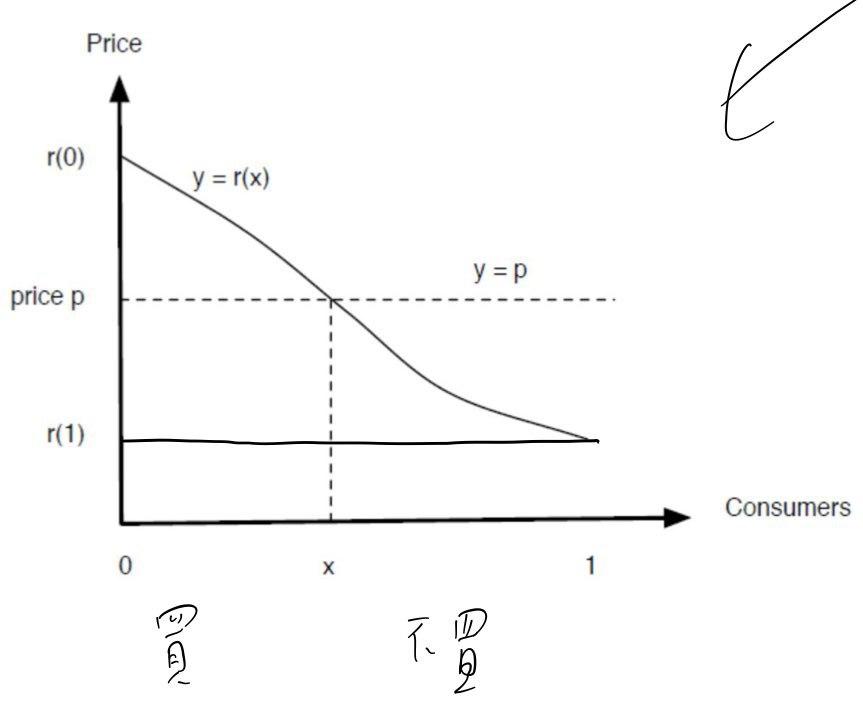
5. p 代表商品的價格， p 是固定值

   1. r(x) > p 就會買
   2. 如果 p > r(0)，就沒人買，因 r(0) 是最大的 reservation price
   3. 如 p < (1)，則所有人都會買，因 r(1) 是最小的 reservation price

6. p* 是固定的生產成本

   1. 每個 producer 只會賣出 p*
   2. 因為在很多 producer 競爭情況下，利益會被拉到幾乎為 0
   3. producer 也不可能貼錢賣
   4. 因此 producer 只能賣 p*

Equillibrium quantity

有一 x* 使 r(x*) = p*，就稱呼 x* 為 equilibrium quantity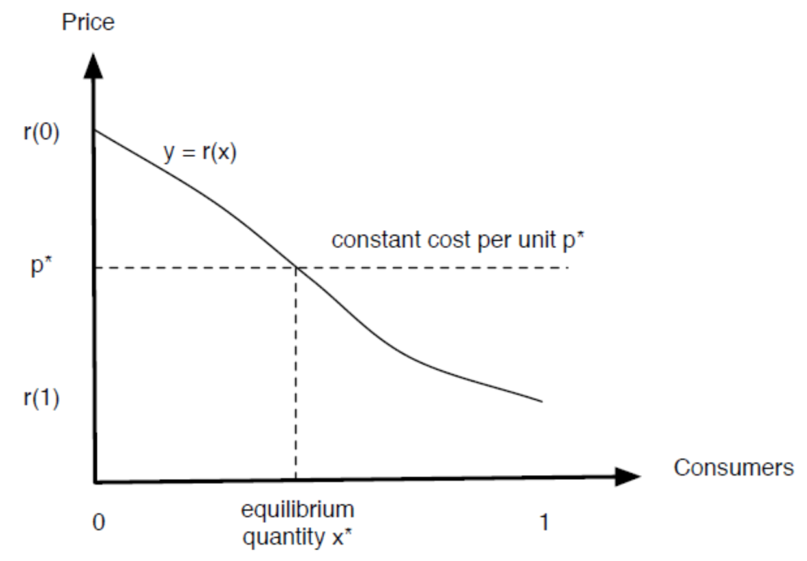

Social optimal

使 每個人的 welfare 加起來最大，就是 social optimal
在不考慮 network effect 的情況下，小於 x* 就買，大於 x* 就不買，就能達到 Social optimal

每個人的 welfare 是 $如 x 買的話 w(x)=r(x)-p^* ，不然 w(x) = 0$
social welfare 是 $\int_0^1w(x)dx$，當此值最大時，就是 social welfare

economy with network effects

當 z% 的總人口使用商品時，獲得 f(z) 的效益，z 是已知的數字，且假設 f(z) = 0
因此 reservation price 變成 r(x)f(z)
為了簡化分析，進一步假設 r(1) = 0

假設商品價值為 p*，那當 r(x)f(z) > p* 時，消費者就會購買

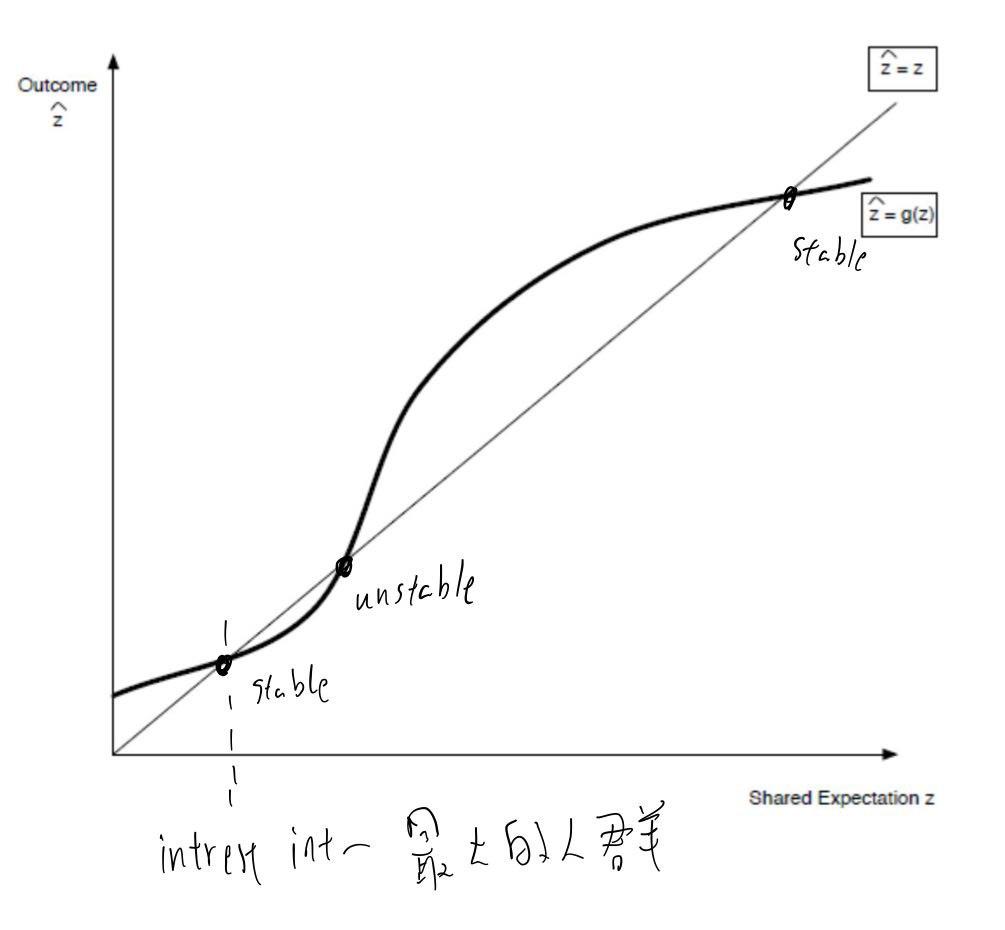
self fulling expectations equilibrium

如果群體有共同期望，那那個期望就會自動成真，很像是 消費者對產品的信心 的總和
例如大家都認為台GG股票價值 100，那台GG的股票價值就會往 100 靠近，直到變成 100
例如大家都認為有 z 人會使用產品，那使用人數就會往 z 靠近，直到變成 z

• z = 0 是 self fulfilled，因為f(x) = 0，所以 r(x)f(x) = 0，因此就沒人會買

• 當 z 在 0~1 之間，

  • r(x*)f(z) = p*
  • 此時會買的人 x 在 0 < x < x*，當 x* 為 z 時，會是 self fulfilled
  • 所以 p* = r(z)f(z)
  • 
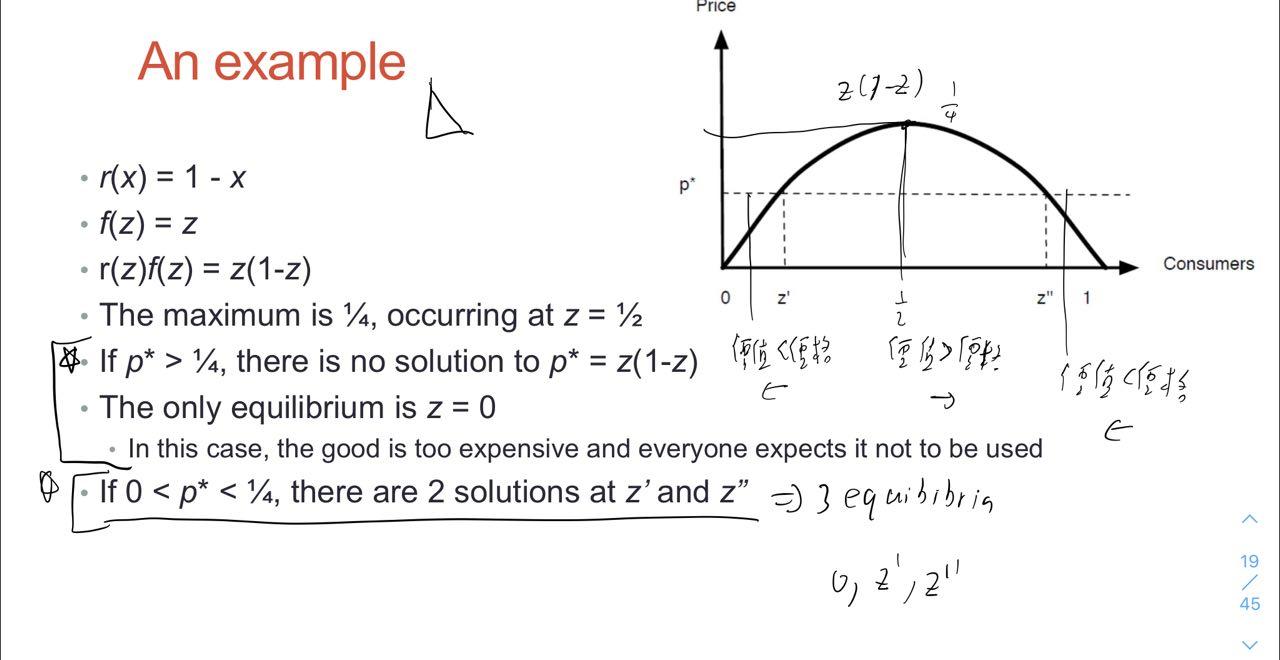
  • 當 p* 移動時， z’ z’’ 也會跟著移動

• 當 z 不在 0 z’ z’’ 上時

  • 0 < z < z’， z 會 往 0 移動 (下降)
  • z’ < z < z’’ ， z 會往 z’’ 移動 (上升)
  • z > z’’， z 會往 z’’ 移動 (下降)

• z’ 是 unstable ，也就是創業門檻，過了門檻之後就會遠離 z’，直奔 z’’ ， 在 z’ 附近會遠離 z'

• z’’ 是 stable ，也可說是市占率，在 z’’ 附近會往 z’’ 靠

• 降低 p* 可以使 z’ 降低，增加 z''

不知道 z 的情況下作分析 - g(z)

• 假設大家有共識 z
• 願意買的人在 0 ~ $\hat{z}$ 中間， $\hat{z} 是購買意願最低的人$，及 $[0,\hat{z}]$
• 推導
  • $r(\hat{z})f(z)=p^*$
  • $r(\hat{z})=\frac{p^*}{f(z)}$
  • $\hat{z}=r^{-1}(\frac{p^*}{f(z)})$
  • 定義 g(z)，輸入 z 時映射到真正會買的人數 $\hat{z}$，所以 g(z) 為
    • 如 $\frac{p^}{f(z)}<=r(0)，g(z)=\hat{z}=r^{-1}(\frac{p^}{f(z)})$
    • 除此之外(p* 太大的情況下)， g(z) = 0
• 

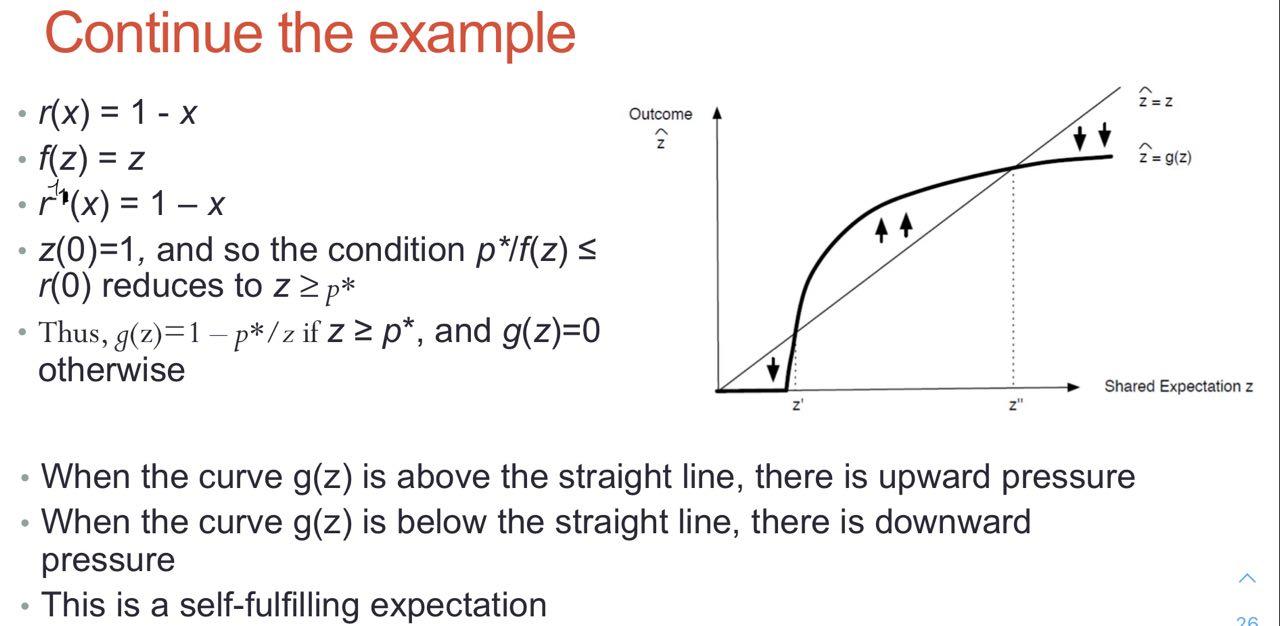
dynamic behavior - 隨時間改變的行為

把交易改成參與社群網路或不參與 - 比交易更動態

z 會隨時間改變，時間是離散的 t = 0 1 2 3 …
當 t=0 時， 會有 $z_0$ 參與

$z_t=g(z_{t-1})$，因為 g 是把預計購買人映射到實際購買人的函數，而 t=t-1階段的實際購買人，會是t=t階段的預計購買人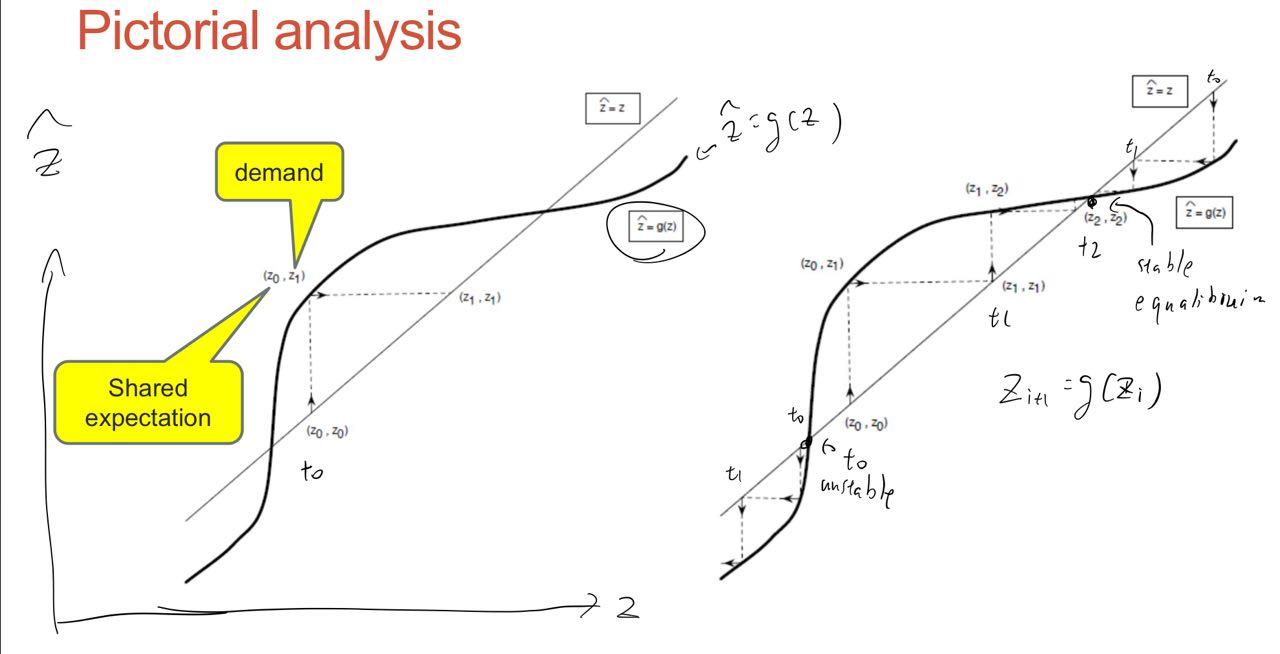

實際產品分析

• 如果 p* 很大，那 z’ 就會很大，因此幾乎不會有東西賣出去

• 降低 p*，讓 z; 近乎於 0，這樣更容易跨過 z’，且 z’‘也更大

• 社群屬性的產品創業要成功，就要跨過 z’(tipping point z’)

• 一開始小量投入是無法做起來的，因為很難跨過 z'

• 所以一開始就要燒錢(賠本賣等等)來跨過 z’，之後把價格漲到能賺錢的地步

• 或是用 fashion leader 來打響知名度(見 ch19)

• 很多時候，產品成不成功是看誰先跨過 tipping point z’，而不是誰品質比較好

Social optimality with network effect

之前我們說， 沒有 network effect 時 ，z* 之前的顧客買就是 social optimality
但是，有 network effect 就不一定是這樣，因為如果強迫 [z*,z*+c) 的人去購買，雖然 [z*,z*+c) 這段會讓 social welfare 下降，但是因為 z*+c 這段會讓整體 network effect 上升，因此上升的可能比下降還多，因此可能會賺更多

$r(x)f(z^)-p^ < r(x)f(z^+c)-p^$ - 這是單個顧客，要做積分才是 social welfare

Mixing individual effect with population-level effect

有些多合一機器，除了 social effect 的功能之外，還有其他能獨立使用的功能，因此 social effect 為 0 時，整體的 Reservation price 不是 0
例如傳真機可以掃描文件等等

• $f(z) = 1+ az^2$，1 就是附加價值，讓 reservation price 在 z=0 時不為 0
• $r(x) = 1-x $
• $如 $r(0)>=\frac{p^}{f(z)}，則 g(z)=r^{-1}(\frac{p^}{f(z)})$，否則 $g(z)=0$
• $g(z) = 1-\frac{p^*}{1+az^2}$