基本性質

• Behavior 互相影響，而不是獨立事件
• popularity 非常不平衡，高的很高，低的很低

檢驗分散程度是否是 normally distributed

實驗證明，發現不是，因 normal 會假設都是 independency，但這裡不是

power law

呈現多項式 $f(k)=\frac{a}{k^c}$

驗證是否為 power law

畫出取 log 的結果，看是不是直線
$\log f(k)=\log a - c \log k$
此時 -c 是斜率， loga 是跟 y 的交點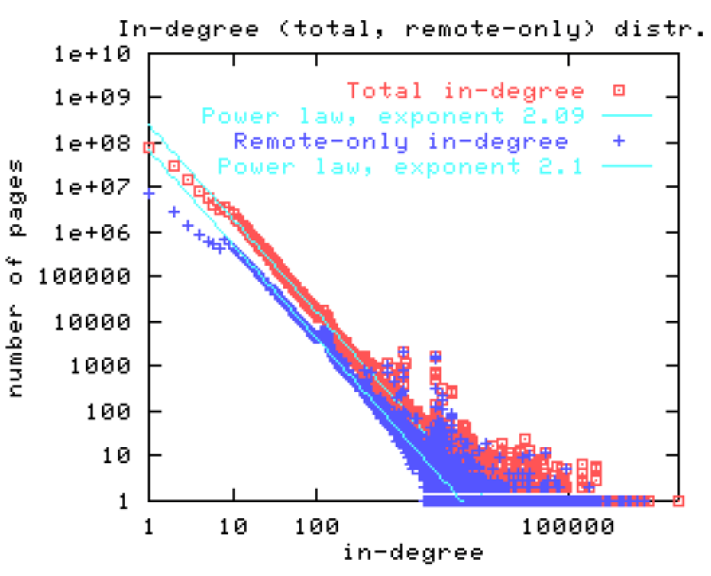

rich-get-richer model

模擬實驗

• decision 不是完全無關

  • information cascade 會影響
  • network effect 也會影響

• pages 是順序生成的，由 page1 page2 … pageN

• 每個 page 只連到一個 page (也可擴充成連到多個 page)

  • 當 page j 生成時，有 p 的機率連到前面生成的其中一個 page i
  • 當 page j 生成時，有 1-p 的機率連到前面生成的其中一個 page i 所連到的 page h
    • 等效於 page h inlink 數量 越大，被連到的機率越高
    • $V_h $= page h inlink 的數量，N 是所有 inlink 的總和
    • page h 被選到的機率為 $\frac{V_h}{N}$

• 1-p 越大，越不平衡

歷史重來，每次暢銷的東西都不相同

會

preferential attachment vs information cascade

• 相同點
  • 兩者都有模仿
• 不同點
  • copy 讓人有比較多選項，IC 只能選擇接受或拒絕
  • copy 只參考一個人決定，IC 是參考所有人決定
  • copy 是盲目 copy，IC 是理性決策

Search Tools 跟推薦系統

1. 大者越大，也叫做 scale free effect
2. 探索讓 rich get richer 效應下降

附註

• 不是所有東西都能 copy，1-p 在城市中，等於人越多生越多

Analysis of Rich-Get-Richer

將 random variable 換成期望值 t+1 時增加的量 $\frac{dx_j(t)}{dt}=\frac{p}{t}+\frac{(1-p)x_j(t)}{t}$